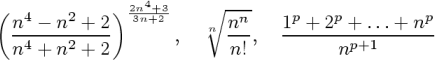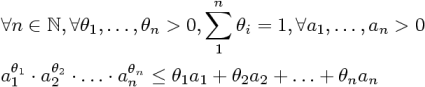Pro Thema war eine Stunde Arbeitszeit vorgesehen.

Klasse 8

Zahlentheorie.

1. Auf welche Ziffer endet 17¹⁴ + 13¹⁷ − 29¹⁸?
2. p₁ und p₂ heißen Primzahlzwilling, falls p₁ und p₂ Primzahlen mit p₂ = p₁ + 2 sind. Beweise, daß für solche Paare mit p₁>3 immer 12 | (p₁+p₂) gilt!

Logik/Mengenlehre.

1. Man vereinfache (¬A₁ ∨ A₂) ∧ (A₂ ∨ A₃) ∧ A₃ soweit wie möglich!
2. [a,b] bezeichnet die Menge aller reellen Zahlen x mit a ≤ x ≤ b. Sei ferner P die Menge aller Primzahlen, N die Menge der natürlichen Zahlen. Man berechne |&weierp(N ∩ [4,10] \ P)|.

Geometrie.

1. In einem Dreieck ABC sind D, E, F die Mittelpunkt der Seiten AB, BC, CA (in dieser Reihenfolge), und M ist der Schnittpunkt der Mittelsenkrechten. Zeige

   |DBM| + |ECM| + |FAM| = |ABC| / 2,

   wobei |XYZ| den Flächeninhalt des Dreiecks XYZ bezeichnet.
2. In einem Dreieck ABC ist W der Schnittpunkt der Winkelhalbierenden, und D, E, F die Fußpunkte der Lote von W auf AB, BC, CA (in dieser Reihenfolge). Zeige

   |DBW| + |ECW| + |FAW| = |ABC| / 2.

Graphentheorie.

1. Untersuche, ob man mit einem Springer alle 7 × 7 = 49 Felder eines Schachbrettes durchlaufen kann, so daß auf jedes Feld genau einmal gesetzt wird und der letzte Zug auf einem dem Ausgangsfeld benachbarten Feld endet.
2. Ist es möglich, eine Rundreise des Springers so zu finden, daß jedes Feld genau einmal berührt wird und der Springer auf das Ausgangsfeld zurückkehrt?

Klasse 9

Unendlichkeit.

Beweise indirekt, daß die Menge aller Teilmengen der natürlichen Zahlen nicht abzählbar ist!

Dreiecke.

Zu konstruieren ist ein Dreieck, in dem die Länge der Seite c, die Länge der Höhe h_a und die der Seitenhalbierenden s_a gegeben ist. Beschreibe die Konstruktion allgemein! Wann ist sie eindeutig ausführbar? Konstruiere das Dreieck für c=5cm, h_a=2.5cm, s_a=3cm!

Induktion.

1. Wieviele Flächen können maximal durch n Kreise entstehen?
2. Wie groß ist die Summe der ersten n natürlichen Zahlen?

Zahlentheorie.

In einem Mathelager spielen alle 40 Teilnehmer gegeneinander Tischtennis (jeder gegen jeden). Kann man nun alle Teilnehmer so hintereinander aufstellen, daß jeder gegen den Vordermann gewonnen und gegen den Hintermann verloren hat?

Klasse 10

Kegelschnitte.

Gegeben sei eine Ellipse mit den Halbachsen a, b, den Brennpunkten F₁, F₂ und ein beliebiger Punkt P₁(x₁, y₁) auf der Kurve. Der Punkt H liege auf der Verlängerung von F₁P₁ über P₁ hinaus. Beweise: Dann ist die Winkelhalbierende des Winkels F₂P₁H gleich der Tangente an die Ellipse im Punkt P₁.

Mittel.

1. Wie ist das Mittel var>n-ten Grades definiert?
2. Wie lauten die Ungleichungen von Bernoulli?
3. Man beweise:

   x³ + y³ + z³ ≥ 3,

   falls x²+y²+z²=3 und x>0, y>0, z>0. Wann gilt die Gleichheit?

Zahlentheorie.

1. Man zerlege die Gaußsche Zahl 4+2i in Gaußsche Primzahlen. Wieviele verschiedene Zerlegungen gibt es?
2. Ist 12600 als Summe zweier Quadrate darstellbar?

Term-Ersetzungs-Systeme.

Wir betrachten das System mit dem Alphabet Σ={T,⋅}, den Stelligkeiten s(T)=0, s(⋅)=2 und der Regelmenge R={ (T ⋅ x)⋅ y → x ⋅ (y ⋅ T) }. Weiter bezeichne k(t) die Anzahl der ⋅ in einem Term t.

1. Beschreibe die Menge der Normalformen.
2. Wenn t' Normalform von t ist, vergleiche k(t') und k(t).
3. Beweise: Wenn t₁ und t₂ Normalformen sind, dann benötigt t₁ ⋅ t₂ genau (2^k(t₁)−1)2^k(t₂) Schritte bis zur Normalform.

Klasse 11/12

Hyperbolische Geometrie.

Man beweise, daß alle Horozyklen kongruent sind.

Analysis.

1. Berechne die Grenzwerte der Zahlenfolgen
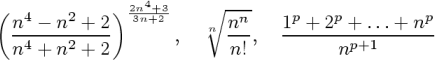
2. Beweise folgende verallgemeinerte Ungleichung zwischen geometrischem und arithmetischen Mittel mittels der Ungleichung von Jensen

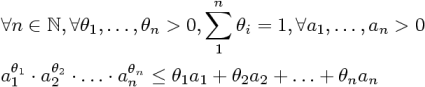
Graphentheorie.

Man zeige, daß in jedem k-zusammenhängenden (k≥2) Graphen G=(V,E) zu jeder k-elementigen Knotenmenge V' ein Kreis in G existiert, der alle Knoten aus V' enthält.

Knoten und Zöpfe.

Durch den Zopf σ = σ₃σ₂σ₁²σ₃^-2 σ₂³σ₃^-1σ₁^-1σ₂^-1σ₃^-1, mit σ ∈ B⁴, ist eine Verschlingung L(σ) definiert.

1. Zeichne ein minimales Diagramm dieser Verschlingung!
2. Sind die Komponenten dieser Verschlingung Primknoten?
3. Sind die Komponenten 3-färbbar? Wenn ja, eine Färbung angeben.
4. Wie groß sind die Entknotungszahlen der einzelnen Komponenten der Verschlingung?